واریانس و انحراف معیار به زبان ساده:
ابتدا اجازه دهید به یک سوال پاسخ دهیم که انحراف معیار چیست؟
انحراف معیار از دو کلمه تشکیل شده است. اولین جزء، انحراف، فاصله هر یک از اعضای مجموعه داده از میانگین است. کلمه استاندارد نیز به معنای معیار ارزش است.
هرچه انحراف معیار مجموعه ای از داده ها کمتر باشد، احتمال اینکه داده ها با انحراف کمی به میانگین نزدیک شوند، بیشتر می شود.
اگر انحراف استاندارد بزرگتر باشد، به این معنی است که داده ها پراکنده تر هستند. بنابراین انحراف معیار عددی است که نشان می دهد اعضای مجموعه ای از داده ها چقدر پراکنده هستند.
انحراف معیار به چه دردی میخورد؟
انحراف معیار مفهومی است که میزان پراکندگی مجموعه ای از داده ها را تعیین می کند و از این رو یکی از مهم ترین معیارهای آماری در حوزه آمار توصیفی به شمار می رود.
اگر میانگین تخمینی از مرکز ثقل توزیع مجموعهای از دادهها ارائه دهد، و در نتیجه مقیاسی تک بعدی برای تخمین مجموعهای از دادهها ارائه دهد، میتوان گفت که انحراف معیار نیز نشان دهنده درجه توزیع است. داده. از میانگین گسترش یافته است، بنابراین مقیاس دو بعدی آن تخمینی از توزیع داده ها را به ما می دهد.
مثال هایی از انحراف معیار
برای مثال، اگر شما یک معلم هستید، ممکن است مهم باشد که بدانید دانشآموزانتان در آزمونی که اخیراً شرکت کردهاید چگونه عمل کردهاند. اگر 20 یا 30 دانش آموز دارید، ممکن است نتوانید عملکرد کل کلاس را با نگاه کردن به نمرات فردی به طور دقیق تخمین بزنید، اما اگر نمرات همه دانش آموزان را میانگین بگیرید، می توانید ایده ای از نحوه کلاس به دست آورید. اجرا کردن کل کار انجام شد.
به عنوان مثال، اگر معدل کلاس برابر با 12.5 باشد و میانگین محاسبه شده از آخرین امتحان 14 باشد، این نشان دهنده افت عملکرد است و باید راه حلی پیدا کرد.
به عنوان یک معلم، بهتر است با کدام دانش آموزان کار کنید؟ البته برای دانش آموزانی که عملکرد بهتری دارند نیازی به تلاش زیاد نیست، اما دانش آموزانی که عملکرد ضعیفی دارند باید توجه ویژه ای داشته باشند.
اما چگونه میدانید که کدام دانشآموزان دارای عملکرد برتر، متوسط یا ضعیف هستند؟ پاسخ به این سوال با محاسبه انحراف معیار است. انحراف معیار معیاری را به ما می دهد که بر اساس آن می دانیم عملکرد یک دانش آموز متوسط چقدر با میانگین کلاس تفاوت دارد.
برای مثال، فرض کنید انحراف استاندارد کلاس شما 2.5 است. اگر توزیع نمرات دانشآموزان نرمال باشد (که در اکثر این معیارها صدق میکند)، این عدد به این معنی است که بیش از دو سوم یا 68.2 درصد از دانشآموزان نمرات در محدوده 2.5+ خواهند داشت. ساعت 12.5 است. این عدد بر اساس تعریف انحراف معیار است.
همچنین یک سوم دانش آموزانی هستند که نمرات 15 به بالا دارند که طبیعتا زحمت زیادی از شما نمی خواهد و یا نمره زیر 10 که البته توجه ویژه شما را می طلبد. بنابراین با محاسبه انحراف معیار نمرات کلاس می توان دانش آموزان را به سه دسته ضعیف (کمتر از 10)، متوسط (10 تا 15) و قوی (بالای 15) تقسیم کرد.
فرض کنید در مثال بالا، تعداد دانش آموزانی که نمره زیر 10 کسب کرده اند (یعنی شکست خورده) برابر با 5 است. همچنین فرض را بر این می گذاریم که معلم این دسته از دانش آموزان را به تمرین می برد، اما معدل کلاس در امتحان بعدی همچنان 12.5 است.
در نگاه اول، تلاش های او بی نتیجه به نظر می رسید. اما با محاسبه انحراف معیار می بینیم که این عدد به 1 کاهش یافته است، یعنی بیش از دو سوم کلاس در محدوده 1+12.5 امتیاز دارند. این به این معنی است که تعداد دانش آموزانی که نمره کمتر از 10 می گیرند احتمالا کاهش یافته است
شاید در نگاه اول به نظر برسد، تلاشهای وی بینتیجه بوده است؛ اما با محاسبه انحراف معیار میبینیم که این عدد به ۱ کاهش یافته است، یعنی نمرات بیش از دوسوم کلاس در محدوده ۱ + ۱۲٫۵ قرار دارد. این به آن معنی است که به احتمال بسیار زیاد تعداد دانشآموزانی که نمره زیر ۱۰ کسب کردهاند، کاهش یافته است.
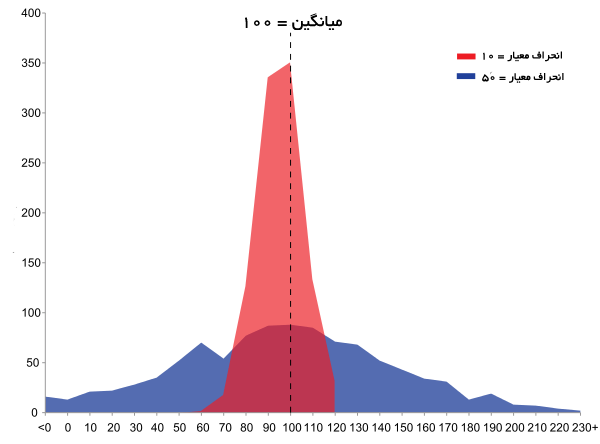
در تصویر فوق به خوبی اهمیت مفهوم انحراف معیار در برآورد توزیع دادهها را میبینید.
هر دو مجموعه دادههای آبی و قرمز رنگ میانگینی برابر با ۱۰۰ دارند ولی انحراف معیار مجموعه دادههای آبی ۵ برابر دادههای قرمز است. علامتی که برای نشان دادن انحراف معیار استفاده میشود، حرف یونانی سیگما ” σ ” است.
روشی که عموماً برای محاسبه انحراف معیار استفاده میشود از طریق جذر گرفتن از واریانس است. خب اکنون شاید بپرسید واریانس چیست؟
واریانس چیست؟
واریانس به صورت «مقدار متوسط مربع اختلاف مقادیر از میانگین» تعریف شده است. شاید در نگاه نخست تعریف دشواری به نظر برسد! اما هیچ جای نگرانی نیست چون در عمل خواهید دید که مفهوم بسیار سادهای است.
برای محاسبه واریانس، باید گامهای زیر را دنبال کنید:
- ابتدا میانگین را پیدا کنید (میانگین ساده اعداد).
سپس برای هر عدد، مقدار میانگین را از آن تفریق کرده و سپس نتیجه را به توان دو برسانید (مربع اختلاف).
و در نهایت میانگین مربع اختلافات به دست آمده را محاسبه کنید.
واریانس دادهها آماده است. به همین سادگی!
مثال
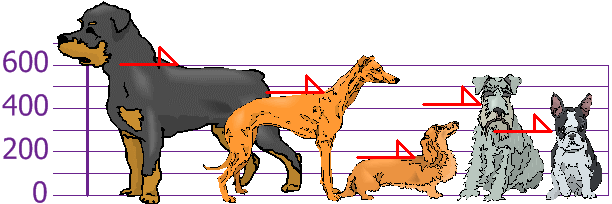
فرض کنید متصدی یک محل نگهداری از سگها میخواهد قد سگهای موجود را به منظور خاصی اندازهگیری کند. نتایج این اندازهگیری قد (از شانه) به شرح زیر است:
۳۰۰، ۴۳۰، ۱۷۰، ۴۷۰ و ۶۰۰ میلیمتر
اینک میخواهیم میانگین، واریانس و انحراف معیار این دادهها را پیدا کنیم. گام اول یافتن میانگین است:

پس میانگین قد همه سگها برابر با ۳۹۴ میلیمتر است. اکنون خط میانگین را روی شکل رسم میکنیم:

اکنون اختلاف قد هر کدام از سگها را از مقدار میانگین حساب میکنیم:
 برای محاسبه واریانس، اختلاف تکتک دادهها را به توان دو رسانده و سپس میانگین میگیریم:
برای محاسبه واریانس، اختلاف تکتک دادهها را به توان دو رسانده و سپس میانگین میگیریم:
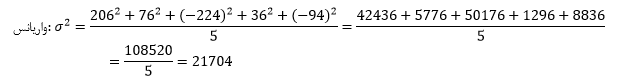
پس، واریانس برابر است با: ۲۱۷۰۴
و انحراف معیار همان جذر واریانس است، پس:
![]()
و اما نکته خوب در مورد انحراف معیار، سودمند بودن آن است. اکنون میتوانیم بفهمیم قد کدام سگها در محدوده یک انحراف معیار میانگین (۱۴۷ میلیمتر) قرار دارد.

بنابراین، با استفاده از انحراف معیار، روشی «استاندارد» برای یافتن محدوده مقادیر نرمال، بالاتر و زیر نرمال داریم.
با این حال، زمانی که به همه اعضای مجموعه دسترسی نداریم، از نمونه برداری استفاده می کنیم.
نمونه گیری به انتخاب تصادفی برخی از اعضا از یک مجموعه بزرگ (که جامعه آماری نامیده می شود) اشاره دارد که در محاسبات آماری به عنوان نمونه نماینده کل نمونه در نظر گرفته می شوند، در این صورت خطای کمتری هنگام محاسبه انحراف معیار و واریانس وجود دارد. تفاوت.
به عنوان مثال، در مورد سگ ها، مجموعه داده های ما به یک گروه مربوط می شود (فقط 5 سگ مورد مطالعه قرار گرفتند).
اما اگر دادههای ما یک نمونه باشد، یک جمعیت کوچک که از یک جمعیت بزرگتر گرفته شده است، مانند 5 سگ که به طور تصادفی از یک جمعیت 50 نفری انتخاب شدهاند، محاسبه تغییر میکند.
وقتی N داده وجود دارد، هنگام محاسبه واریانس، مجموع مجذور تفاوت میانگین ها را بر N تقسیم کنید.
با این حال، هنگامی که این محاسبات بر روی یک نمونه جامعه آماری انجام می شود، مجموع اختلاف مجذور میانگین ها بر N-1 تقسیم می شود. در این صورت بقیه محاسبات از جمله روش محاسبه میانگین بدون تغییر باقی می مانند.
مثال: اگر ۵ سگ موجود فقط نمونهای از جمعیت بزرگتر سگها باشد، مقدار را به جای ۵، باید بر ۴ تقسیم کنیم:
واریانس نمونه: ۱۰۸۵۲۰/۴ = ۲۷۱۳۰
انحراف معیار نمونه = ۲۷۱۳۰√ = ۱۶۴ (نزدیکترین داده)
دلیل این منهای یک کردن، خارج از حوصله این نوشته است و برای اطلاعات بیشتر میتوانید به لینکهای انتهای نوشته مراجعه کنید.
فرمولها:
در ادامه فرمولهای ریاضی حالت کلی محاسبه انحراف معیار برای هر دو حالت جمعیت و نمونه آماری ارائه شده است:
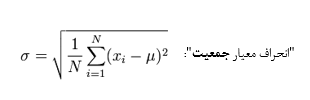

گرچه پیچیده به نظر میآید، اما ما قبلاً آن را به طرز بسیار سادهای محاسبه کردهایم. تنها تفاوت مهم، تقسیمبر N-1 (بجای N) هنگام محاسبه واریانس نمونه است.
چرا اختلاف از میانگینها را به توان دو میرسانیم؟
اگر ما تنها اختلافها را میانگینگیری میکردیم… اعداد منفی، اعداد مثبت را خنثی میکردند:

پس این راهحل درست نیست. اما آیا از قدر مطلق مقادیر میتوانیم استفاده کنیم؟

همانطور که میبینید به نظر میرسد انحراف میانگین به طور صحیحی محاسبه شده است؛ اما در مورد حالت زیر چه میتوان گفت؟

میبینید که مقدار انحراف معیار همچنان ۴ محاسبه شده است، در حالی که اختلاف میانگینها بسیار پراکندهتر است.
در نهایت میبینیم که مربع کردن هر اختلاف و محاسبه جذر در آخر روش بهتری محسوب میشود.
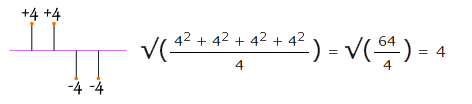

البته در تحلیل آماری شاید محاسبات دستی انجام نشود و با کمک نرم افزار هایی مانند spss و spls و غیره انجام می شود.


دیدگاه ها